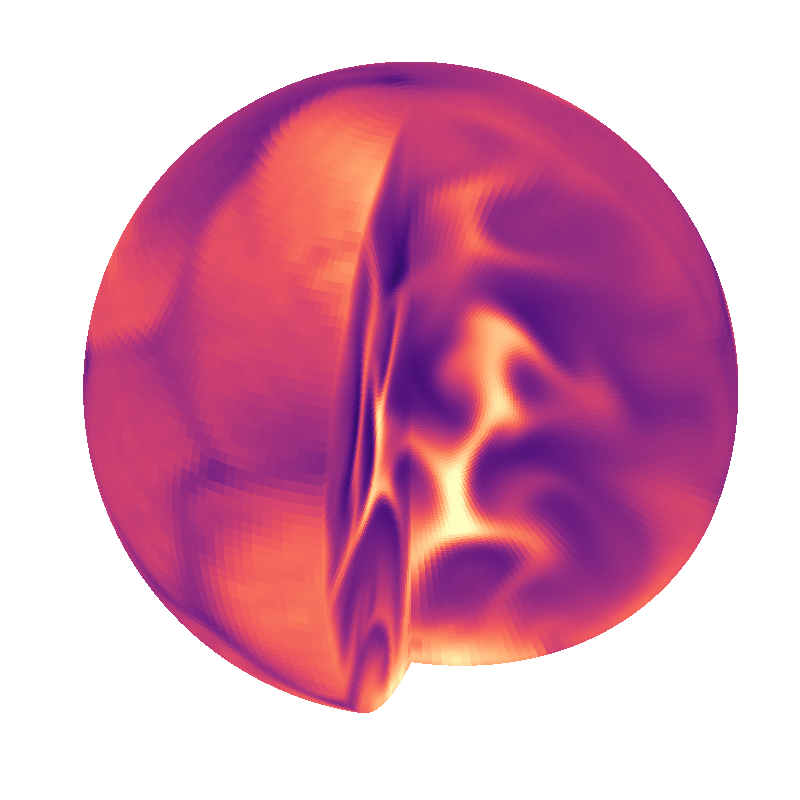
"""
Dedalus script simulating internally-heated Boussinesq convection in the ball.
This script demonstrates soving an initial value problem in the ball. It can be
ran serially or in parallel, and uses the built-in analysis framework to save
data snapshots to HDF5 files. The `plot_ball.py` script can be used to produce
plots from the saved data. The simulation should take roughly 30 cpu-minutes to run.
The strength of gravity is proportional to radius, as for a constant density ball.
The problem is non-dimensionalized using the ball radius and freefall time, so
the resulting thermal diffusivity and viscosity are related to the Prandtl
and Rayleigh numbers as:
kappa = (Rayleigh * Prandtl)**(-1/2)
nu = (Rayleigh / Prandtl)**(-1/2)
We use stress-free boundary conditions, and maintain a constant flux on the outer
boundary. The convection is driven by the internal heating term with a conductive
equilibrium of T(r) = 1 - r**2.
For incompressible hydro in the ball, we need one tau term each for the velocity
and temperature. Here we choose to lift them to the original (k=0) basis.
The simulation will run to t=20, about the time for the first convective plumes
to hit the top boundary. After running this initial simulation, you can run the
simulation for an addition 20 time units with the command line option '--restart'.
To run, restart, and plot using e.g. 4 processes:
$ mpiexec -n 4 python3 internally_heated_convection.py
$ mpiexec -n 4 python3 internally_heated_convection.py --restart
$ mpiexec -n 4 python3 plot_ball.py slices/*.h5
"""
import sys
import numpy as np
import dedalus.public as d3
import logging
logger = logging.getLogger(__name__)
# Allow restarting via command line
restart = (len(sys.argv) > 1 and sys.argv[1] == '--restart')
# Parameters
Nphi, Ntheta, Nr = 128, 64, 96
Rayleigh = 1e6
Prandtl = 1
dealias = 3/2
stop_sim_time = 20 + 20*restart
timestepper = d3.SBDF2
max_timestep = 0.05
dtype = np.float64
mesh = None
# Bases
coords = d3.SphericalCoordinates('phi', 'theta', 'r')
dist = d3.Distributor(coords, dtype=dtype, mesh=mesh)
ball = d3.BallBasis(coords, shape=(Nphi, Ntheta, Nr), radius=1, dealias=dealias, dtype=dtype)
sphere = ball.surface
# Fields
u = dist.VectorField(coords, name='u',bases=ball)
p = dist.Field(name='p', bases=ball)
T = dist.Field(name='T', bases=ball)
tau_p = dist.Field(name='tau_p')
tau_u = dist.VectorField(coords, name='tau u', bases=sphere)
tau_T = dist.Field(name='tau T', bases=sphere)
# Substitutions
phi, theta, r = dist.local_grids(ball)
r_vec = dist.VectorField(coords, bases=ball.radial_basis)
r_vec['g'][2] = r
T_source = 6
kappa = (Rayleigh * Prandtl)**(-1/2)
nu = (Rayleigh / Prandtl)**(-1/2)
lift = lambda A: d3.Lift(A, ball, -1)
strain_rate = d3.grad(u) + d3.trans(d3.grad(u))
shear_stress = d3.angular(d3.radial(strain_rate(r=1), index=1))
# Problem
problem = d3.IVP([p, u, T, tau_p, tau_u, tau_T], namespace=locals())
problem.add_equation("div(u) + tau_p = 0")
problem.add_equation("dt(u) - nu*lap(u) + grad(p) - r_vec*T + lift(tau_u) = - cross(curl(u),u)")
problem.add_equation("dt(T) - kappa*lap(T) + lift(tau_T) = - u@grad(T) + kappa*T_source")
problem.add_equation("shear_stress = 0") # Stress free
problem.add_equation("radial(u(r=1)) = 0") # No penetration
problem.add_equation("radial(grad(T)(r=1)) = -2")
problem.add_equation("integ(p) = 0") # Pressure gauge
# Solver
solver = problem.build_solver(timestepper)
solver.stop_sim_time = stop_sim_time
# Initial conditions
if not restart:
T.fill_random('g', seed=42, distribution='normal', scale=0.01) # Random noise
T.low_pass_filter(scales=0.5)
T['g'] += 1 - r**2 # Add equilibrium state
file_handler_mode = 'overwrite'
initial_timestep = max_timestep
else:
write, initial_timestep = solver.load_state('checkpoints/checkpoints_s20.h5')
initial_timestep = 2e-2
file_handler_mode = 'append'
# Analysis
slices = solver.evaluator.add_file_handler('slices', sim_dt=0.1, max_writes=10, mode=file_handler_mode)
slices.add_task(T(phi=0), scales=dealias, name='T(phi=0)')
slices.add_task(T(phi=np.pi), scales=dealias, name='T(phi=pi)')
slices.add_task(T(phi=3/2*np.pi), scales=dealias, name='T(phi=3/2*pi)')
slices.add_task(T(r=1), scales=dealias, name='T(r=1)')
checkpoints = solver.evaluator.add_file_handler('checkpoints', sim_dt=1, max_writes=1, mode=file_handler_mode)
checkpoints.add_tasks(solver.state)
# CFL
CFL = d3.CFL(solver, initial_timestep, cadence=10, safety=0.5, threshold=0.1, max_dt=max_timestep)
CFL.add_velocity(u)
# Flow properties
flow = d3.GlobalFlowProperty(solver, cadence=10)
flow.add_property(u@u, name='u2')
# Main loop
try:
logger.info('Starting main loop')
while solver.proceed:
timestep = CFL.compute_timestep()
solver.step(timestep)
if (solver.iteration-1) % 10 == 0:
max_u = np.sqrt(flow.max('u2'))
logger.info("Iteration=%i, Time=%e, dt=%e, max(u)=%e" %(solver.iteration, solver.sim_time, timestep, max_u))
except:
logger.error('Exception raised, triggering end of main loop.')
raise
finally:
solver.log_stats()